John Conway's Game Of Life

The Game of Life, also known simply as Life, is a cellular automaton devised by the British mathematician John Horton Conway in 1970.

The "game" is a zero-player game, meaning that its evolution is determined by its initial state, requiring no further input. One interacts with the Game of Life by creating an initial configuration and observing how it evolves or, for advanced players, by creating patterns with particular properties.

Rules

The universe of the Game of Life is an infinite two-dimensional orthogonal grid of square cells, each of which is in one of two possible states, alive or dead. Every cell interacts with its eight neighbours, which are the cells that are horizontally, vertically, or diagonally adjacent. At each step in time, the following transitions occur:

Any live cell with fewer than two live neighbours dies, as if caused by under-population.

Any live cell with two or three live neighbours lives on to the next generation.

Any live cell with more than three live neighbours dies, as if by over-population.

Any dead cell with exactly three live neighbours becomes a live cell, as if by reproduction.

The initial pattern constitutes the seed of the system. The first generation is created by applying the above rules simultaneously to every cell in the seed—births and deaths occur simultaneously, and the discrete moment at which this happens is sometimes called a tick (in other words, each generation is a pure function of the preceding one). The rules continue to be applied repeatedly to create further generations.

Ever since its publication, Conway's Game of Life has attracted much interest, because of the surprising ways in which the patterns can evolve. Life provides an example of emergence and self-organization. Scholars in various fields, such as computer science, physics, biology, biochemistry, economics, mathematics, philosophy, and generative sciences have made use of the way that complex patterns can emerge from the implementation of the game's simple rules[citation needed]. The game can also serve as a didactic analogy, used to convey the somewhat counter-intuitive notion that "design" and "organization" can spontaneously emerge in the absence of a designer. For example, philosopher and cognitive scientist Daniel Dennett has used the analogue of Conway's Life "universe" extensively to illustrate the possible evolution of complex philosophical constructs, such as consciousness and free will, from the relatively simple set of deterministic physical laws governing our own universe.

The popularity of Conway's Game of Life was helped by its coming into being just in time for a new generation of inexpensive minicomputers which were being released into the market. The game could be run for hours on these machines, which would otherwise have remained unused at night. In this respect, it foreshadowed the later popularity of computer-generated fractals. For many, Life was simply a programming challenge: a fun way to use otherwise wasted CPU cycles. For some, however, Life had more philosophical connotations. It developed a cult following through the 1970s and beyond; current developments have gone so far as to create theoretic emulations of computer systems within the confines of a Life board.

Examples of Patterns

Game of Life Patterns

The earliest interesting patterns in the Game of Life were discovered without the use of computers.

The simplest static patterns ("still lifes") and repeating patterns ("oscillators"—a superset of still lifes) were discovered while tracking the fates of various small starting configurations using graph paper, blackboards, physical game boards (such as Go) and the like.

During this early research, Conway discovered that the R-pentomino failed to stabilize in a small number of generations. In fact, it takes 1103 generations to stabilize, by which time it has a population of 116 and has fired six escaping gliders (these were the first gliders ever discovered).

Many different types of patterns occur in the Game of Life, including still lifes, oscillators, and patterns that translate themselves across the board ("spaceships"). Some frequently occurring examples of these three classes are shown below, with live cells shown in black, and dead cells shown in white.

Still Lifes

Oscillators

Spaceships

Block

Blinker (period 2)

Glider

Beehive

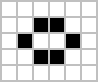Toad (period 2)

Lightweight spaceship

Loaf

Beacon (period 2)

Boat

Pulsar (period 3)

The Code

\ Game of Life - TurboForth Version
\ ported from:
\ http://www.forth-ev.de/wiki/doku.php/projects:4e4th:4e4th:start:beispiele)

DECIMAL
16 CONSTANT #lines
8 CELLS CONSTANT b/cell  \ bits per cell: = number of columns

: line  ( n -- a-addr ) CELLS pad + ;
: lrot  ( x1 -- x2 )  \ rotate left by one
   DUP 2* SWAP 0< - ;
: lrot3  ( x1 x2 x3 --  x4 x5 x6 ) lrot ROT  lrot ROT  lrot ROT ;

HERE  0 C, 1 C, 1 C, 2 C,  1 C, 2 C, 2 C, 3 C,  CONSTANT #bits
: countbits  ( x -- n )  \ count number of bits=1 in bit0..2
   7 AND #bits + C@ ;

: alive  ( x1 x2 x3 -- flag )
   \ return whether cell at bit1 in line1 is alive in next generation
   OVER 2 AND 0= NOT >R
   countbits
   SWAP countbits +  \ note: cell itself is counted, too. correction below.
   SWAP countbits +
   DUP 3 =  SWAP 4 = R> AND OR ;
   
: 3dup  ( x1 x2 x3 -- x1 x2 x3 x1 x2 x3 )
   2 pick 2 pick 2 pick ;
   
: doline  ( x1 x2 x3 -- x1 x2 x3 x4 )
   0  b/cell 0 DO 
      >R   3dup alive 2 AND R> OR lrot >R
      lrot3   R>
   LOOP ;
   
: nextgen  ( -- )
   0 line @   #lines 1- line @  OVER   ( s: line0   x1 x2 )
   #lines 1- 0 DO
      I 1+ line @               ( s: line0  x1 x2 x3 )
      doline  I line !
      ROT DROP                  ( s: line0  x2 x3 )
   LOOP  
   ROT doline  #lines 1- line !   \ special treatment for last line
   2DROP DROP ;
   
: .line  ( x -- )
   b/cell 0 DO
      DUP 0< IF ASCII @  ELSE ASCII . THEN EMIT
      lrot
   LOOP  DROP ;
   
VARIABLE generation 
: .universe  ( -- )  \ print current life state to console 
    0 0 gotoxy 
   #lines 0 DO   CR I line @ .line  LOOP cr 
   generation @ .  1 generation +! ;
   
: life  ( -- ) \ run life with output to console, until key <q> pressed
   1 gmode BEGIN
      .universe     nextgen  
   key? ascii q = until ;

: void  ( -- )  pad #lines CELLS 0 FILL ;
: seed  ( x1 .. xn n -- )   0 DO i line ! LOOP ;
HEX   \ some wellknown patterns:
: glider  ( -- )  7 1 2  3 seed ;
: fpent  ( -- )  4 0C 6  3 seed ;
: lwss  ( -- )  0F 11 1 12  4 seed ;
: diehard  47 0C0 2  3 seed ;
: acorn  67 8 20  3 seed ;
: demo   glider   700 3 line ! ;
DECIMAL

void demo life

John Conway's Game Of Life

Rules

Examples of Patterns

The Code

Aknowledgements